0%

时间序列分析及预测基础

发表于 Valine：
本文字数： 5.4k 阅读时长 ≈ 5 分钟

数据分析的架构（3A）：

  • Data Aggregation
  • Data Analysis
  • Data Activation

时间序列分析与回归分析的区别:

  • 在选择模型前，我们需要确定结果与变量之间的关系。回归分析训练得到的是目标变量y与自变量x（一个或者多个）的相关性，然后通过新的自变量x来预测目标变量y。而时间序列分析得到的是目标变量y与时间的相关性。
  • 回归分析擅长的是多变量与目标结果之间的分析，即便是单一变量，也往往与时间无关。而时间序列分析建立在事件变化的基础上，它会分析目标变量的趋势、周期、时期和不稳定因素等。这些趋势和周期都是在时间维度的基础上，是我们要观察的重要特征。

时间序列：

  • 机器学习模型， 包括AR、MA、ARMA、ARIMA
  • 神经网络模型， 用LSTM进行时间序列预测

时间序列及分解：

  • 平稳序列(stationary series)
    基本上不存在趋势(Trend)的序列，各观察值基本上在某个固定的水平上波动
  • 非平稳序列(non-stationary series)
    包含趋势、季节性或周期性的序列，可以只有一种成分，也可能是多种成分的组合
  • 趋势(trend)
    时间序列在长时间内呈现出来的某种持续上升或者持续下降的变动，也称为长期趋势。
  • 季节性(seasonality)
    时间序列在一年内重复出现的周期性波动。销售旺季，销售淡季，旅游旺季，旅游淡季。季节可以是任何一种周期性的变化，不一定是一年中的四季，含有季节成分的序列可能含有趋势，也可能不含有趋势。
  • 周期性(cyclicity)
    通常是由经济环境的变化引起的不同于趋势变动，不是朝着单一方向的持续性运动，而是涨落相间的交替波动。不同于季节变动，季节变动有比较固定的规律， 变动周期大多为一年。周期性的循环波动无固定规律，变动周期大多在一年以上，且周期长短不一。
  • 随机性(irregular)
    指受偶然因素影响所形成的的不规则性波动，在时间序列中无法预估。除去趋势、周期性、季节性的偶然性波动。
因素 举例
长期趋势 Trend(T) 国内生产总值
季节变动 Season(S) 冰淇淋、羽绒服、裙子等
周期性 Cyclic(C) 太阳黑子数量变化
随机性 Irregular(I) 股票市场突然的利好、利空等信息的影响

时间序列工具（statsmodels）

statsmodels主要包括如下子模块：

  • 回归模型：线性回归，广义线性模型，线性混合效应模
  • 方差分析(ANOVA)
  • 时间序列分析: AR, MA, ARMA, ARIMA等

AR模型

  • Auto Regressive, 中文叫自回归模型
  • 认为过去若干时刻的点通过线性组合，再加上白噪声就可以预测未来某个时刻的点
  • 日常生活环境中就存在白噪声，在数据挖掘的过程中，可以把它理解为一个期望为0，方差为常数的纯随机过程。
  • AR模型存在一个阶数p, 称为AR(p)模型，也叫做p阶自回归模型。指的是通过这个时刻点的前p个点，通过线性组合再加上白噪声来预测当前时刻点的值。
  • AR是线性时间序列分析模型中最简单的模型，通过前面部分的数据与后面部分的数据之间的相关关系来建立回归方程：
    $x_t = φ1x{t-1}+φ2x{t-2}+…+φpx{t-p}+φ1x{t-1}+u_t$
    AR(p),表示p阶的自回归过程，$φ$为自回归系数，$u_t$表示白噪声，是时间序列中数值的随机波动。这些波动会相互抵消，即累计为0
  • 如果只有一个时间记录点时，则为AR(1),即一阶自回归过程：
    $x_t = φ1x{t-1}+φ1x{t-1}$

MA模型

  • Moving Average(滑动平均模型)
  • 与AR模型大同小异， AR模型是历史时序值的线性组合+白噪声，MA是通过历史白噪声进行线性组合来影响当前时刻点
  • MA模型中的历史白噪声通过影响历史时序值，从而间接影响到当前时刻的预测值
  • MA模型存在一个阶数q,称为MA(q)模型，也叫做q阶移动平均模型
  • AR与MA模型都存在阶数，在AR模型中，用p表示，在MA模型中，用q表示，这两个模型大同小异，与AR模型不同的是MA模型是历史白噪声的线性组合
  • MA模型， 通过将前面一段时间序列中的白噪声序列进行加权求和，可以得到移动平均方程：
    $x_t = u_t + φ1u{t-1}+φ2u{t-2}+…+φqu{t-q}$
  • MA(q)表示q阶移动平均过程，$φ$为移动回归系数，$u_t$为不同时间点的白噪声
  • $x_t$为第t天的股票价格，$u_t$为第$t$天的新闻影响，当天的价格受当天新闻的影响，也受昨天新闻的影响

ARMA模型

  • Auto Regressive Moving Average(自回归滑动平均模型)
  • AR模型和MA模型的混合，相比AR模型和MA模型，它有更准确的估计
  • ARMA模型存在$p$和$q$两个阶数，称为ARMA(p, q)模型，它有更准确的估计
    $x_t =u_t + φ1u{t-1}+φ2u{t-2}+…+φqu{t-q}+θ1x{t-1}+θ2x{t-2}+…+θpx{t-p}$
  • 自回归滑动平均模型结合了两个模型的特点，AR解决当前数据与前期数据之间的关系，MA则可以解决随机变动，即噪声问题

ARIMA模型

  • Auto Regressive Integrated Moving Average模型，中文叫差分自回归滑动平均模型，也叫求和自回归滑动平均模型
  • 相比于ARMA，ARIMA多了一个差分的过程，作用是对不平稳数据进行差分平稳，在差分平稳后再进行建模
  • ARIMA的原理和ARMA模型一样。相比于ARMA(p,q)的两个阶数，ARIMA是一个三元组的阶数（p,d,q），称为ARIMA(p,d,q)模型，其中d是差分阶数
  • AR,MA是ARMA的特殊形式，而ARMA是ARIMA的特殊形式
  • ARIMA模型步骤：
    • Step1, 观察时间序列数据，判断是否为平稳序列
    • Step2, 对于非平稳时间序列要先进行d阶差分运算，化为平稳时间序列
    • Step3, 使用ARIMA（p,d,q）模型进行训练拟合，找到最优的（p,d,q）,及训练好的模型
    • Step4, 使用训练好的ARIMA模型进行预测，并对差分进行还原
  • ARIMA用差分将不平稳数据先变得平稳，再用ARIMA模型

关于差分：

  • 差分=序列之间做差值，目的是得到平稳的序列，也就是去掉前面数值的影响
  • 一次差分为序列之间做一次差值，二次差分为在一次差分的基础上再做一次差分
  • $f(x) = x^2$ 若x=[1, 4, 9, 11, …] (x有二次趋势)
  • 一次差分的结果为[4-1, 9-4, 16-9, 25-16 …] = [3, 5, 7, 9, 11, …], 此时x序列仍然不平稳，有一次上升的趋势，再做一次差分为[2,2,2,2…],此时x为平稳序列

ARMA工具

  • from statsmodels.tsa.arima_model import ARMA
  • ARMA(endog, order, exog = None)
  • endog: endogenous variable, 代表内生变量， 又叫非政策性变量， 它是由模型决定的， 不被政策左右，可以说是我们想要分析的变量， 或者说是我们这次项目中需要用到的变量
  • order: 代表p和q的值，也就是ARMA中的阶数
  • exog: exogenous variables, 代表外生变量。外生变量和内生变量一样是经济模型中的两个重要变量。相对于内生变量而言， 外生变量又称作政策性变量， 在经济体制内受外部因素的影响，不是我们模型要研究的变量，如果我们想要创建ARMA（7，0）模型，可以写成ARMA(data,(7,0))，其中data是我们要观察的变量，(7,0)代表(p,q)的阶数。
  • fit函数，进行拟合
  • predict(start, end)函数，进行预测，其中start为预测的起始时间，end为预测的终止时间。

ARIMA(p, d, q)阶数确定：

模型 ACF PACF
AR(p) 衰减趋于零(几何型或振荡型) p阶后截尾
MA(q) q阶后截尾 衰减趋于零(几何型或振荡型)
ARMA(p,q) q阶后衰减趋于零(几何型或振荡型) p阶后衰减趋于零(几何型或振荡型)
截尾： 落在置信区间内（95%的点后符合该规则） 
1
2
3
4
5
6
# 用ARMA进行时间序列预测
import statsmodels.api as sm
from statsmodels.tsa.arima_model import ARMA
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 创建数据
data = [
    3821, 4236, 6783, 4664, 2589, 2538, 3542, 4626, 5886, 6233, 4199, 3561,
    2335, 5636, 3524, 4327, 6064, 3912, 1356, 4305, 4379, 4592, 4233, 4281,
    1613, 1233, 4514, 3431, 2159, 2322, 4239, 4733, 2268, 5397, 5821, 6115,
    6631, 6474, 4134, 2728, 5753, 7130, 7860, 6991, 7499, 5301, 2808, 6755,
    6658, 6944, 6372, 8380, 7366, 6352, 8333, 8281, 11548, 10823, 13642, 9973,
    6723, 13416, 12205, 13942, 9590, 11693, 9276, 6519, 6863, 8237, 10122,
    8646, 9749, 5346, 4836, 9806, 7502, 9387, 11078, 9832, 6886, 4285, 8351,
    9725, 11844, 12387, 10666, 7072, 6429, 7777
]
print(len(data))
data = pd.Series(data)

data_index = sm.tsa.datetools.dates_from_range('1901', '1990')
90
1
2
3
4
# 绘制数据图
data.index = pd.Index(data_index)
data.plot(figsize=(12, 8))
plt.show()

png

1
2
3
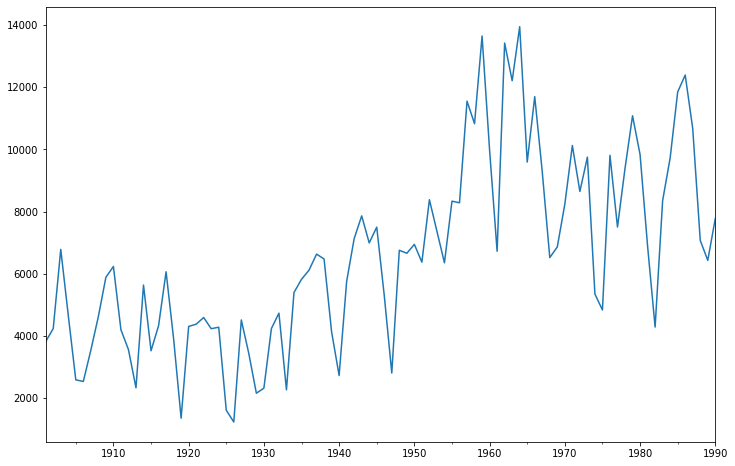
# 创建ARMA模型
arma=ARMA(data,(7,0)).fit()
print('AIC:%0.4f'%arma.aic)
C:\Users\Administrator\Anaconda3\lib\site-packages\statsmodels\tsa\base\tsa_model.py:162: ValueWarning: No frequency information was provided, so inferred frequency A-DEC will be used.
  % freq, ValueWarning)


AIC:1615.3524
1
2
3
4
5
6
7
# 模型预测
predict_y = arma.predict('1990', '2000')
# 预测结果绘制
fig, ax = plt.subplots(figsize=(12, 8))
ax=data.loc['1901':].plot(ax=ax)
predict_y.plot(ax=ax)
plt.show()

png

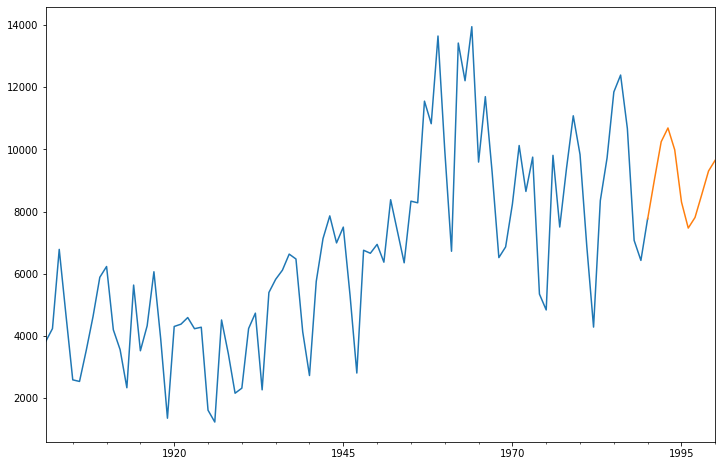
使用ARMA工具对沪市指数进行预测：

  • Step1, 数据加载&探索
    按照不同的时间尺度（天，月，季度，年）可以将数据压缩，得到不同时间尺度的数据，然后做可视化呈现。在这4个时间尺度上，我们选择“月”作为预测模型的时间尺度。

    1
    df_month = df.resample('M').mean()

  • Step2,模型选择&训练，在给定范围内，选择最优超参数
    创建ARMA时间序列模型。我们并不知道p和q取什么值时模型最优，因此可以给它们设定一个区间范围，然后使用网格搜索，计算不同模型的AIC数值，选择AIC最小时的模型

  • Step3,模型预测，可视化呈现
    采用该ARMA模型预测未来3个月的沪市指数走势，并将结果做可视化呈现。

LSTM:

  • LSTM, Long Short-Term Memory, 长短期记忆网络
  • 可以避免常规RNN的梯度消失，在工业界有广泛应用
  • 引入了三个门函数：输入门（Input Gate）、遗忘门（Forget Gate）和输出门（Output Gate）来控制输入值、记忆值和输出值
  • 输入门决定当前时刻网络的状态有多少信息需要保存到内部状态中；遗忘门决定了过去的状态信息有多少需要丢弃=>输入门和遗忘门是LSTM能够记忆长期依赖的关键
  • 输出门决定当前时刻的内部状态有多少信息需要输出到外部状态
    一个LSTM单元在每个时间步会接受三个输入：
  • $x_t$:当前时刻的输入
  • $h_{t-1}$:上一时刻的外部状态
  • $c_{t-1}$:上一时刻的内部状态
    $x_t$和$h_{t-1}$同时作为三个门的输入,$б$是Logistic函数

image.png

1
2


谢谢老板！祝老板越来越大！